< Предыдущая 1 ... 8 9 10 11 12 ... 47 Следующая > 

События. Теоремы сложения и умножения

Решения задач с 3472 по 3521

Задача 3472. Студентка Иванова подготовила 25 билетов из 30-ти. Найти вероятность того, что с 3-ей попытки она возьмет «счастливый билет».

Задача 3473. Вероятность безотказной работы каждого элемента в течение времени Т равна р. Элементы работают независимо и включены в цепь по приведенной схеме. Пусть событие Аi означает безотказную работу за время Т элемента с номером i (i= 1,2,3,...),а событие B – безотказную работу цепи. Требуется:
5.1) Написать формулу, выражающую событие B через событие Аi
5.2) Найти вероятность события B
5.3) Вычислить P(B) при р=1/2

Задача 3474. Вычислить надежность схемы, полагая, что надежность круглых элементов равна 0,9, прямоугольных – 0,8 и треугольных – 0,75.

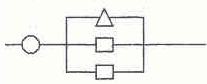
Задача 3475. Рабочий обслуживает одновременно 4 независимо работающих станка. Вероятность того, что в течение часа станок не остановится, равна для первого станка 0,9, для второго 0,8, для третьего 0,7, для четвертого 0,75. Определить вероятность того, что по крайней мере один станок в течение часа будет работать без остановок.

Задача 3476. Три стрелка одновременно стреляют по мишени. Вероятность попадания для первого стрелка равна 1/5, для второго 1/6, для третьего 1/6. Найти вероятность:
А) того, что в мишень попадет только один стрелок;
Б) хотя бы одного попадания.

Задача 3477. Испытание состоит в подбрасывании 3-ех монет. Сколько раз нужно провести испытание, чтобы с вероятностью не менее 0,95 хотя бы один раз появились «три решки»?

Задача 3478. Рабочий обслуживает три станка, работающие независимо друг от друга. Вероятность того, что в течение часа первый станок не потребует внимания рабочего, равна 0,9, для второго станка такая вероятность равна 0,8, для третьего станка - 0,85. Какова вероятность того, что в течение часа
а) ни один из станков не потребует внимания рабочего,
б) какой-нибудь один станок потребует внимания рабочего,
в) хотя бы один станок потребует внимания рабочего.

Задача 3479. Два игрока поочередно извлекают шары (без возвращения) из урны, содержащей 1 белый и 4 черных шара. Выигрывает тот, кто первым вытащит белый шар. Найти вероятности выигрыша для каждого игрока.

Задача 3480. Случайным образом выбирается число из множества S={1,2,3,4,5,6,7,8,9}. Событие А={взятое число <5}, В={взятое число >6}. Используя теорему сложения, найдите вероятность того, что взятое число принадлежит хотя бы одному множеству А или В.

Задача 3481. Станок-автомат штампует детали. Вероятность того, что за смену не будет выпущено ни одной нестандартной детали, равна 0,9. Определить вероятность того, что за две смены не будет выпущено ни одной нестандартной детали.

Задача 3482. Два стрелка, для которых вероятности попадания в мишень равны соответственно 0,7 и 0,8 , производят по одному выстрелу. Определить вероятность хотя бы одного попадания в мишень.

Задача 3483. Среди 25 экзаменационных билетов 5 “хороших”. Два студента по очереди берут по одному билету. Найти вероятность того, что
а) первый студент взял хороший билет;
б) второй студент взял хороший билет;
в) оба взяли хорошие билеты.

Задача 3484. Имеется две урны, в первой из которых 7 белых и 4 черных шара, во второй – 3 белых и 5 черных. Найти вероятность того, что если выбрать из каждой урны по шару, оба они окажутся белыми.

Задача 3485. Найти вероятность хотя бы одного появления события А в 10 независимых опытах, если вероятность появления А в каждом опыте равна 0,1.

Задача 3486. По данным одного из участков станции технического обслуживания автомобилей деталь А заменяется в среднем в 36% случаев, деталь В – в 42% случаев, а одновременно детали А и В подлежат замене в среднем в 30 % случаев аварий автомобилей.
а) Зависят ли одна от другой замена деталей А и В?
б) Найти вероятность того, что деталь В будет заменена, если деталь А уже заменена.

Задача 3487. Разыскивая специальную книгу, студент решил обойти три библиотеки. Для каждой библиотеки одинаково вероятно есть ли в ее фондах книга или нет. И если книга есть, то одинаково вероятно занята она другим читателем или нет. Что более вероятно - достанет ли студент книгу или нет, если известно, что библиотеки комплектуются независимо друг от друга?

Задача 3488. Два стрелка стреляют в одну цель. Вероятность поражения цели первым стрелком - 0,8; вторым - 0,5. Стрелки стреляют по команде один раз. Найти вероятность того, что цель будет поражена хотя бы одним из стрелков.

Задача 3489. Мишень состоит из десяти кругов, ограниченных концентрическими окружностями с радиусами r_k (k=1, 2, ..., 10); причем r₁ < r₂ < ... < r₁₀. Событие A_k - попадает в круг радиуса r_k (k=1, 2, ..., 10). Что означают события .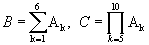

Задача 3490. События А и В несовместимы, Р(А)≠0 и Р(В)≠0. Зависимы ли данные события?

Задача 3491. Событие В является частным случаем события А, т.е. из появления события В с достоверностью вытекает появление событие А. чему равны:
1) их сумма;
2) их произведение?

Задача 3492. Найти вероятность по данным вероятностям: Р(А)=а, Р(В)=b, Р(А+В)=с.

Задача 3493. Изделие последовательно проходит три ступени контроля качества. Вероятности обнаружения дефекта на этих ступенях равны соответственно 0,5, 0,6 и 0,7. Найти вероятность обнаружения дефекта, если контроль прекращается при первом его обнаружении.

Задача 3494. Для взятия веса штангисту дается три попытки. Штангист берет вес с одной попытки с вероятностью 0,9. Какова вероятность того, что понадобятся все 3 попытки?

Задача 3495. Вероятность попадания в мишень равна 1/3. Стрельба прекращается при первом попадании. Найти вероятность, что будет произведено 3 выстрела.

Задача 3496. На спортивных соревнованиях вероятность показать рекордный результат для первого спортсмена равна 0,5; для второго – 0,3; для третьего – 0,1. Какова вероятность того, что: а) рекорд будет установлен одним спортсменом; б) рекорд будет установлен хотя бы одним спортсменом; в) рекорд не будет установлен.

Задача 3497. Вероятность попадания стрелком в мишень - 0,4. Какова вероятность поражения мишени с двух выстрелов?

Задача 3498. Имеется 20 экзаменационных билетов, из которых студент выучил только половину. Какова вероятность сдать экзамен, если на экзамене предоставляются две попытки вытянуть билет?

Задача 3499. Вероятность попадания при выстреле первым стрелком 0,8, вторым — 0,5, третьим – 0,6. Какова вероятность поражения мишени двумя стрелками?

Задача 3500. В урне содержится 8 чёрных, и 6 белых шаров. Случайным образом вынимают 3 шаров. Найти вероятность того, что среди них имеется:
А) 3 белых шара;
Б) меньше, чем 3 белых шара;
В) хотя бы один белый шар.

Задача 3501. Устройство состоит из трёх независимых элементов работающих в течение времени T безотказно соответственно с вероятностями p1, p2 и p3. Найти вероятность того, что за время T выйдет из строя:
А) только один элемент;
Б) хотя бы один элемент.

Задача 3502. СМО - речной порт, в котором три причала. Вероятности того, что в случайный момент времени причал занят, равны: для 1-го причала 0,9; для 2-го - 0,8; для 3-го - 0,7. Найти вероятности того, что в случайный момент времени:
а) все три причала заняты;
б) занят только один причал;
в) хотя бы один причал свободен.

Задача 3503. Пусть события A, B и C - произвольные случайные события. Выразить через операции с этими событиями события, состоящие в том, что:
А) произошло, по крайней мере, два из этих событий;
Б) произошло два и только два из этих событий;
в) произошло не больше двух из этих трех событий.

Задача 3504. Вероятность попадания в цель для первого стрелка равна 0,7, а для второго – 0,8. Стрелки выстрелили одновременно. Какова вероятность того, что лишь один из них попадет в цель? Какова вероятность того, что первый стрелок попадет в цель?

Задача 3505. Вероятность попасть в самолет равна 0,4, а вероятность его сбить равна 0,1. Найти вероятность того, что при попадании в самолет он будет сбит.

Задача 3506. Два спортсмена участвуют в отборочных соревнованиях. Вероятность зачисления в сборную команду первого, второго спортсменов соответственно равны 0,7 и 0,9. Найти вероятность того, что:
а) два спортсмена попадут в сборную,
б) хотя бы один из них попадет в сборную.

Задача 3507. Пусть A, B, C – три произвольных события. Найти выражения для событий, состоящих в том, что из A, B, C:
а) произошли только события В и С;
б) произошло одно и только одно событие;
в) хотя бы одно из трёх событий не произошло.
Привести геометрическую интерпретацию полученных выражений.

Задача 3508. Вероятность попадания в цель для первого стрелка равна 0,8, для второго – 0,7, для третьего – 0,9. Каждый стрелок делает по одному выстрелу. Какова вероятность того, что в мишени хотя бы одна пробоина?

Задача 3509. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равна 0,9, второе – 0,95, третье – 0,85. Найти вероятность того, что при аварии сработает:
А) только одно устройство;
Б) только два устройства;
В) все три устройства;
Г) хотя бы одно устройство.

Задача 3510. Вероятности наступления каждого из двух независимых событий соответственно равны 0,6 и 0,4. Найти вероятность наступления хотя бы одного из них.

Задача 3511. Имеется 3 ящика, содержащих по 40 деталей. В первом ящике 32, во втором 28 и в третьем 24 стандартных деталей. Из каждого ящика вынимают наугад по одной детали. Найти вероятность того, что из трех вынутых деталей две будут стандартными, а одна нестандартной.

Задача 3512. Два стрелка, для которых вероятности попадания в мишень равны соответственно 0,7 и 0,8, производит по одному выстрелу. Определить вероятность хотя бы одного попадания в цель.

Задача 3513. Вероятность потери письма в почтовом отделении равна 0,03, а телеграммы – 0,01. Отправлено два письма и одна телеграмма. Какова вероятность того, что дойдет: а) только телеграмма; б) хотя бы одно из отправлений?

Задача 3514. Для студентов, едущих на практику, представлено 15 мест в Находке, 10 мест в Хабаровске и 5 мест в Уссурийске. Какова вероятность того, что 3 определённых студента попадут на практику в один город?

Задача 3515. Для сигнализации об аварии установлены 3 независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство - 0,95; второе – 0,9; третье – 0,85. Найти вероятность того, что при аварии будет подан сигнал.

Задача 3516. Цепь состоит из двух параллельно соединенных элементов. Вероятность отказа 1-го элемента равна 0,2, 2-го элемента – 0,1. Найти вероятность того, что в цепи будет протекать ток.

Задача 3517. В аптечном складе установлены два датчика предельно допустимой концентрации паров органических растворителей. Вероятность безотказной работы первого датчика равна Р1=0,9, второго Р2=0,9. Найти вероятность событий:
1) Сработает хотя бы один датчик,
2) Сработают оба датчика.

Задача 3518. В клетке n1 белых и n 2 серых мышей. Случайным образом извлекают 3-х мышей. Вычислить вероятность для 4-х возможных комбинаций цвета мышей:
n1=9 n2=8 А1 =(ббб) А2 = (ссс) А3 =(бсс) А4 = (ббс)

Задача 3519. В клетке n1 белых и n 2 серых мышей. Случайным образом извлекают 3-х мышей. Вычислить вероятность для 4-х возможных комбинаций цвета мышей:
А1 =(ббб) А2 = (ссс) А3 =(бсс) А4 = (ббс), где n1=6 n2=3.

Задача 3520. В аптечном складе установлены два датчика предельно допустимой концентрации паров органических растворителей. Вероятность безотказной работы первого датчика равна Р1=0,93, второго Р2=0,96. Найти вероятность событий:
1) Сработает хотя бы один датчик,
2) Сработают оба датчика.

Задача 3521. Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента F1(t)=1-e^-0,1t; для второго F2(t)=1-e^-0,2t, для третьего элемента F3(t)=1-e^-0,3t. Найти вероятность того, что в интервале времени 0,5 ч. откажут:
А) только один элемент;
б) только два элемента;
В) все три элемента.

< Предыдущая 1 ... 8 9 10 11 12 ... 47 Следующая > 

* Конечная стоимость зависит от комиссии выбранного вами варианта оплаты и будет указана перед оплатой.