< Предыдущая 1 ... 11 12 13 14 15 ... 47 Следующая > 

События. Теоремы сложения и умножения

Решения задач с 3624 по 3679

Задача 3624. Вероятность того, что при независимом осмотре больного первый врач допустит ошибку – 0,01, второй – 0,02, третий – 0,015 . Какова вероятность того, что ни один из врачей не допустит ошибки?

Задача 3625. Из тщательно перемешанного полного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую наудачу извлеченную кость можно приставить к первой, если первая кость:
А) оказалась дублем,
Б) не является дублем.

Задача 3626. Вероятность попадания в цель равна 0,003. Сколько нужно произвести выстрелов, чтобы с вероятностью большей 0,94 можно было утверждать, что цель будет поражена?

Задача 3628. Два стрелка независимо выстрелили по мишени по два раза. Меткость первого стрелка равна 0,8; второго – 0,7. Найти вероятность того, что в мишень:
А) попадет хотя бы одна пуля;
Б) попадут все четыре пули.

Задача 3629. Вероятность поражения мишени при одном выстреле первым стрелком равна 0,8, а вторым 0,9. Найти вероятность того, что оба стрелка поразят мишень.

Задача 3630. В мастерской два мотора работают независимо друг от друга. Вероятность того, что в течение часа первый мотор не потребует внимания мастера, равна 0.9: для второго - 0.85. Найти вероятность того, что ни один из моторов не потребует внимания мастера.

Задача 3631. Два спортсмена пытаются выполнить норму мастера спорта. Вероятность того, что первый выполнит норму – 0,85; второй – 0,9. Найти вероятность того, что норма мастера спорта будет выполнена: 1) одним из них; 2) хотя бы одним из них.

Задача 3632. Вероятность для стрелка поразить 1-ю мишень равна 0,45, 2-ю мишень – 0,6 и 3-ю – 0,75. Найти вероятность того, что стрелок при выполнении этих трех заданий не поразил только одну мишень.

Задача 3633. Какова вероятность того, что наудачу взятая дробь сократится на 2, на 5?

Задача 3634. Подбрасываются три игральные кости. Установить, зависимы или независимы события:
А - появится не менее двух единиц,
В - появится не более двух шестерок.
Вычислить условную вероятность P(B/А).

Задача 3635. Подбрасываются три игральные кости. Какова вероятность того, что хотя бы на одной из них выпадет одно очко, если на всех трех костях выпали разные грани? Найти вероятность того, что на всех трех костях выпали разные грани, если известно что на одной из них выпала единица.

Задача 3636. Четыре охотника договорились стрелять по дичи в определенной последовательности. Следующий охотник производил выстрел лишь в случае промаха предыдущего. Вероятность попадания в цель каждым охотником равна 0,8. Найти вероятность того, что будет произведено: а) один, б) два, в) три, г) четыре выстрела.

Задача 3637. Для трех спортсменов вероятность выполнить квалификационную норму равна соответственно 0,8; 0,7; 0,9. Найти вероятность того, что
а) по крайней мере один спортсмен выполнил квалификационную норму;
б) два спортсмена выполнят квалификационную норму.

Задача 3638. Трое исследователей следят за показаниями приборов независимо друг от друга. Вероятности допустить ошибку первым, вторым и третьим соответственно равны 0,18; 0,15; 0,12. Найти вероятности того, что хотя бы один исследователь допустит ошибку при измерениях.

Задача 3639. Сколько раз надо повторить испытание чтобы с вероятностью не меньшей r утверждать, что хотя бы один раз произойдет событие А, вероятность появления которого в каждом опыте равна 0,8.

Задача 3642. Трое поочередно бросают монету. Выигрывает тот, у кого раньше появиться герб. Определить вероятности выигрыша для каждого из игроков.

Задача 3643. Производится независимая стрельба по аэростату. Вероятность попадания при одном выстреле равна 0,05. Сколько нужно произвести выстрелов, чтобы вероятность сбить аэростат при n выстрелов была больше 0,8.

Задача 3644. При включении зажигания двигатель начинает работать с вероятностью Р.
А) Найти вероятность того, что двигатель начнет работать при втором включении зажигания.
Б) Найти вероятность того, что для ввода двигателя в работу придется включать зажигание не более 2 раз.

Задача 3645. Брошены три игральные кости. Чему равна вероятность того, что на одной из них выпала единица, если на всех трех костях выпали разные числа.

Задача 3646. Два истребителя независимо друг от друга атакуют боевой порядок противника, в составе которого 6 носителей и 3 поставщика помех, внешне неразличимых. Определить вероятность того, что хотя бы один истребитель атаковал носитель.

Задача 3647. Колода из 52 карт сдается поровну 4-м игрокам. Какова вероятность того, что при 3-х последовательных сдачах определенный игрок не получит ни одного туза?

Задача 3648. Найти вероятность прохождения тока через цепь, если вероятности исправной работы элементов указаны на схеме. Элементы работают независимо друг от друга.

Задача 3649. Прибор состоит из 3-х узлов. Вероятность отказа в течение времени t для каждого узла равна 0,2. Найти вероятность того, что за время t откажет хотя бы один узел.

Задача 3650. Произведено два выстрела по цели. Вероятность попадания в цель при каждом выстреле равна 0,7. Найти вероятность поражения цели.

Задача 3651. В горном районе создано автоматических сейсмических станций. Каждая станция в течение года может выйти из строя с вероятностью p. Какова вероятность того, что в течение года хотя бы одна станция потребует ремонта.

Задача 3652. Аппаратчик химического завода обслуживает три установки. Вероятность работы без ремонта в течение смены у первой установки равна 0,7, у второй установки – 0,8 и у третьей – 0,6. Найти вероятность того, что за смену хотя бы одна установка потребует ремонта.

Задача 3653. Наугад вынимается одна карта из 36. Событие
А - вытащенная карта – туз,
В - вытащенная карта черного цвета,
С - вытащенная карта – фигура.
Определить, зависимы ли события А и В, А и С, В и С.

Задача 3654. В 1-ом ящике 6 шаров - 1 белый, 2 красных и 3 синих, во 2-ом ящике 12 шаров - 2 белых, 6 красных и 4 синих. Из каждого ящика вынули по 1 шару. Какова вероятность, что среди вынутых нет синих?

Задача 3656. ДВероятность поражения стрелком мишени при каждом выстреле равна p. Найти вероятность того, что число последовательных (подряд) промахов будет оставаться меньше трёх в течение
а) трёх выстрелов;
б) четырёх выстрелов;
в) пяти выстрелов.

Задача 3657. Пусть А, В, С – три произвольных события. Найти выражения для событий, состоящих в том, что из А, В, С:
а) произошли только события А и В;
б) произошло по крайней мере одно событие;
в) произошло более двух событий.
Привести геометрическую интерпретацию полученных выражений.

Задача 3658. Найти вероятность Р(АВ) по данным вероятностям: Р(А)=а, Р(В)=b, Р(А+В)=с.

Задача 3659. Вероятность попадания в цель для первого стрелка равна 0,85, для второго - 0,75, для третьего – 0,9. Каждый стрелок делает по одному выстрелу. Какова вероятность того, что в мишени хотя бы 1 пробоина?

Задача 3660. Какова вероятность появления хотя бы одного герба при подбрасывании двух монет?

Задача 3661. Испытываются три прибора на надежность. Вероятности выхода из строя каждого соответственно равны 0,2; 0,3; 0,4. Найти вероятность, что из строя выйдут 2 прибора (безразлично какие).

Задача 3662. Известно, что 5% от радиоламп, изготовляемых заводом, являются нестандартными. Из большой партии производится случайная выборка радиоламп. Сколько ламп надо взять, чтобы с вероятностью не менее 0,9 была извлечена хотя бы одна нестандартная лампа?

Задача 3663. Вероятность попадания в мишень при каждом выстреле для первого стрелка равна 0,7, а для второго — 0,8. Оба они делают по одному выстрелу по мишени, а затем каждый из стрелков стреляет еще раз, если при первом выстреле он промахнулся. Найти вероятность того, что в мишени ровно две пробоины.

Задача 3664. Проведено 20 независимых испытаний, каждое из которых заключается в одновременном подбрасывании 3-х монет. Найдите вероятность того, что хотя бы в одном испытании выпадут 3 герба.

Задача 3665. Телефонистка трижды вызывает абонента. Вероятность того, что будет принят первый вызов, равна 0,2, второй вызов – 0,3 и третий вызов – 0,4. В предположении независимости вызовов друг от друга найти вероятность того, что абонент услышит вызов.

Задача 3666. Два стрелка попадают в цель при одном выстреле с вероятностями равными, соответственно, 0.6 и 0.8. Найти вероятность хотя бы одного попадания в цель при одном залпе.

Задача 3667. Люся Копейкина знает ответы только на 15 билетов из 30. Когда ей лучше идти вынимать билет: первой, второй или последней?

Задача 3668. Вероятность отказа за время Т каждого элемента равна Р. Элементы работают независимо и включены в цепь по схеме:

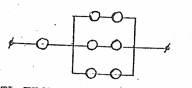
Найти вероятность прекращения тока в цепи за время Т. Предполагается, что отказ элемента ведет к прекращению тока через него.

Задача 3669. Вероятность безотказной работы в течение времени Т каждого элемента равна Р. Элементы работают независимо и включены по схеме (см.ниже). Найти вероятность, что в течение времени Т ток в цепи не прекратится.

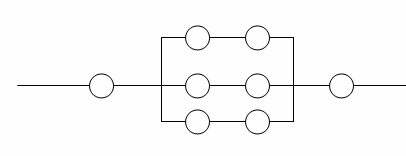
Задача 3670. Вероятность того, что поступившая с первого станка деталь высшего качества 0.7, со второго 0.8, с третьего 0.9. Какова вероятность того, что из трех поступивших деталей только одна деталь высшего качества?

Задача 3672. На книжной полке стоят трехтомник А.С. Пушкина и пятитомник А.П. Чехова. Событие Ak : с полки взят k-ый том Пушкина; Bi : взят i-ый том Чехова. Записать формулами события:
1) среди взятых 5-ти книг не более 2-х томов Пушкина;
2) все 5 книг – Чехова.

Задача 3673. Каждый сотый человек – дальтоник. Сколько надо взять людей, чтобы вероятность встретить среди них хотя бы одного дальтоника была не меньше 0,95?

Задача 3674. Найти вероятности указанных событий, пользуясь правилами сложения и умножения вероятностей.
Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,3. Найти вероятность того, что из трех проверенных изделий только два будут высшего сорта.

Задача 3676. Известны вероятности независимых событий A,B,C: P(A)=0.5, P(B)=0.4, P(C)=0.3.
Определить вероятность того, что:
А) произойдет, по крайней мере, два из этих событий;
Б) ни одного события не произойдет.

Задача 3677. Три последовательно соединенных элемента выходят из строя с вероятностями 0,3; 0,4; 0,6 соответственно. Найти вероятность того, что в цепи будет разрыв.

Задача 3678. Пусть А, В, С, D – четыре произвольных события. Найти выражения для событий, состоящих в том, что из А, В, С, D:
а) произошли только события А и С;
б) произошло по крайней мере три события;
в) произошло не более двух событий.
Привести геометрическую интерпретацию полученных выражений.

Задача 3679. Найти вероятность Р(-A*-B) по данным вероятностям: Р(А)=а, Р(В)=b, Р(А+В)=с.

< Предыдущая 1 ... 11 12 13 14 15 ... 47 Следующая > 

* Конечная стоимость зависит от комиссии выбранного вами варианта оплаты и будет указана перед оплатой.