< Предыдущая 1 2 3 4 5 6 ... 47 Следующая > 

События. Теоремы сложения и умножения

Решения задач с 3153 по 3205

Задача 3153. Три стрелка делают по одному выстрелу в цель. Вероятности попадания в цель соответственно равны 0,6; 0,85; 0,7. Какова вероятность попадания в цель:
а) только второго стрелка;
б) хотя бы одного стрелка?

Задача 3154. Вероятность того, что стрелок при одном выстреле выбьет 10 очков, равна 0,1; вероятность выбить 9 очков равна 0,3; вероятность выбить 8 или меньше очков равна 0,6. Найти вероятность того, что при одном выстреле стрелок выбьет не менее 9 очков.

Задача 3155. Имеется 3 ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.

Задача 3156. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8; p2 = 0,7; p3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий. (

Задача 3157. В мешке смешаны нити, среди которых 30% красных, 60% синих, а остальные белые. Какова вероятность того, что три вынутые наудачу нити будут одного цвета?

Задача 3158. Вероятность дозвониться с первой попытки в справочное бюро вокзала равна 0,4. Какова вероятность того, что
а) удастся дозвониться при втором звонке;
б) придётся звонить не более трёх раз?

Задача 3159. На АТС могут поступать вызовы трех типов. Вероятность поступления вызовов 1-го, 2-го и 3-го типа соответственно равна 0,2; 0.3; 0,5. Поступило 3 вызова. Какова вероятность того, что: а) все они разных типов; б) среди них нет вызова 2-го типа?

Задача 3160. Найти вероятность отказа схемы предполагая, что отказы отдельных элементов независимы. Вероятность отказа каждого элемента равна q.
.

Задача 3161. Вероятности успешной сдачи экзамена по первому, второму и третьему предметам у данного студента соответственно равны 0,6, 0,7 и 0,75. Найти вероятность того, что он успешно сдаст все экзамены.

Задача 3162. Два студента ищут нужную книгу в магазинах. Вероятность того, что книга будет найдена первым студентом, равна 0,6, а вторым – 0,7. Какова вероятность того, что
А) только один из студентов найдет книгу?
Б) хотя бы один из них найдет книгу?

Задача 3163. По мишени производится 3 выстрела. Рассматриваются события Ai - попадание при i-ом выстреле (i=1,2,3). Представьте в виде сумм, произведений или сумм произведений событий следующие события:
А – все 3 попадания;
В – все 3 промаха;
С – хотя бы 1 попадание;
D – хотя бы один промах;
Е – не меньше 2 попаданий;
F – не больше 1 попадания;
G – попадание в мишень не раньше, чем при третьем выстреле

Задача 3164. Имеется 5 электролампочек. Подключение их в сеть и вероятность выхода из строя указаны на чертеже. Определить вероятность того, что в цепи будет ток.

Задача 3165. Два стрелка произвели по одному выстрелу по мишени. Вероятность поражения мишени каждым из стрелков равна 0,8. Найти вероятность того, что:
1) оба стрелка поразят мишень;
2) оба стрелка промахнутся;
3) только один стрелок поразит мишень;
4) хотя бы один из стрелков поразит мишень.

Задача 3166. В урне находится 15 белых, 10 черных и 3 синих шара. Каждые испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что:
а) при первом испытании появится белый шар (событие А), при втором – черный (событие в) и при третьем – синий (событие С);
б) при первом испытании появится белый шар, а при втором и третьем – черные шары.

Задача 3167. Станция метрополитена оборудована тремя эскалаторами, работающими независимо друг от друга. Вероятность безотказной работы в течение рабочего дня первого эскалатора равна 0,97, второго – 0,95, третьего 0,91. Найти вероятность того, что в течение рабочего дня произойдет поломка
А) не более чем одного эскалатора,
Б) хотя бы одного эскалатора.

Задача 3168. Стреляют 3 стрелка в мишень. Вероятность попадания каждого p1=0.6, p2=0.7, p3=0.8. Найти вероятность, что два стрелка попали.

Задача 3169. В двух партиях k1 и k2% доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них:
а) хотя бы одно бракованное;
б) два бракованных;
в) одно доброкачественное и одно бракованное?
k1=72; k2=46.

Задача 3170. Вероятность того, что цель поражена при одном выстреле первым стрелком - p1, вторым - p2. Первый сделал n1, второй - n2 выстрелов. Определить вероятность того, что цель не поражена.
p1=0.64; p2=0.52; n1=3; n2=2.

Задача 3171. Два игрока A и B поочередно бросают монету. Выигравшим считается тот, у кого раньше выпадет герб. Первый бросок делает игрок A, второй – B, третий – A и т.д.
1. Найти вероятность того, что A выиграл до k броска.
2. Каковы вероятности выигрыша для каждого игрока при сколь угодно длительной игре?
k=7

Задача 3172. Бросается игральная кость. Событие А состоит в том, что выпавшее число очков четное. Событие В состоит в том, что выпавшее число очков делится на 3. В чем состоят события А, АВ, А+В.

Задача 3173. Игрок набрасывает кольца на колышки до первого попадания. Вероятность попадания при одном броске равна 0,2. Найти вероятность того, что из пяти колец хотя бы одно останется неизрасходованным.

Задача 3174. Вероятность выигрыша по одному лотерейному билету равна 0.01. Сколько нужно купить билетов, чтобы выиграть хотя бы по одному из них с вероятностью p≥0.95.

Задача 3176. Пятнадцать экзаменационных билетов содержат по два вопроса, которые не повторяются. Студент может ответить только на 25 вопросов. Определить вероятность того, что экзамен будет сдан, если для этого достаточно ответить на два вопроса из одного билета или на один вопрос из первого билета и на указанных дополнительный вопрос из другого билета.

Задача 3177. Два стрелка сделали по одному выстрелу по мишени. Известно, что вероятность попадания в мишень для одного из стрелков равна 0,6, а для другого – 0,7. Найти вероятность того, что хотя бы один из стрелков попадет в мишень?

Задача 3178. В ящике 10 красных и 6 синих пуговиц. Вынимаются науда¬чу две пуговицы. Какова вероятность того, что пуговицы будут одноцветными?

Задача 3180. Доказать, что если А и В — независимые события с положительными вероятностями, то они совместны.

Задача 3182. Пусть А, В, С - три события, наблюдаемые в данном эксперименте. Выразить следующие события через события A, В и С:
D = {ни одно из трех событий А, В, С не произойдет);
Е = {из трех событий А, В, С произойдет ровно одно};
F = {из трех событий произойдет ровно два);
G = {из трех событий произойдет хотя бы одно};
Н = {из трех событий произойдет не менее двух}.

Задача 3183. Вероятность безотказной работы блока в течение заданного времени равна 0,8. Для повышения надежности устанавливается такой же резервный блок. Найти вероятность безотказной работы системы с резервным блоком.

Задача 3184. Три стрелка попадают в мишень с вероятностями 0,85; 0,8; 0,7. Найти вероятность того, что при одновременном выстреле всех трех стрелков в мишени будут пробиты два отверстия.

Задача 3185. Последовательно бросают две монеты и рассматривают следующие события: А-выпадение «орла» на первой монете, В - выпадение хотя бы одной «решки». Определить условную вероятность события А.

Задача 3186. Два стрелка в одинаковых и независимых условия произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 0,7, а вторым – 0,8. Найти вероятность того, что:
А) цель поражена,
Б) цель поражена только одним из стрелков,
В) цель поражена дважды.

Задача 3187. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равна 0,9, второе - 0,95, третье - 0,85. Найти вероятность того, что при аварии сработает:
а) только одно устройство;
б) только два устройства;
в) все три устройства.

Задача 3188. Вероятность попадания в цель для первого стрелка равна 0.8, для второго 0.7, для третьего 0.9. Каждый из стрелков делает по одному выстрелу. Какова вероятность того, что в мишени 3 пробоины?

Задача 3189. Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 0,9, вторым - 0,8, третьим - 0,7. Найти вероятность того, что:
а) только один из стрелков попадет в цель;
б) только два стрелка попадут в цель;
в) все три стрелка попадут в цель.

Задача 3190. Секретарь по просьбе директора звонит в кассу аэровокзала с целью забронировать билет, но успевает сделать не более четырех звонков. Найти вероятность того, что она сделает более двух звонков, если вероятность дозвониться до кассы с одного звонка равна 0,8.

Задача 3191. Три стрелка сделали по выстрелу в мишень. Вероятность попадания в мишень для первого стрелка равна 0,5, для второго - 0,6, для третьего - 0,7. Какова вероятность того, что в мишень попали ровно две пули?

Задача 3192. Для производственной практики на тридцать пять студентов института туризма представлено 15 мест в Санкт-Петербурге, 15 – в Москве и 5 – в Хельсинки. Найти вероятность того, что три определенные студентки попадут на практику в один город.

Задача 3193. Швейное изделие состоит из 3 частей. Вероятности брака при изготовлении каждой из частей соответственно равны 0,1, 0,05, 0,02. Какова вероятность того, что изделие не будет бракованным?

Задача 3194. Рабочий обслуживает 5 станков. 20% времени он уделяет первому станку, 10% - второму, 15% - третьему, 25% - четвёртому и 30% - пятому. Какова вероятность того, что случайно заглянувший в цех мастер, найдёт рабочего у первого, второго или у третьего станка?

Задача 3195. В двух группах обучается по 25 студентов. В первой группе сессию на «отлично» сдали 7 человек, во второй - 4 человека. Из каждой группы наудачу вызывают по одному студенту. Какова вероятность того, что:
а) оба студента отличники;
б) только 1 отличник;
в) хотя бы 1 отличник.

Задача 3196. Вероятность того, что событие А появится хотя бы один раз в трёх испытаниях равна 0,936. Считая что во всех испытаниях вероятность наступления события А постоянная, найти вероятность того, что событие А наступит один раз в двух испытаниях.

Задача 3197. В магазин от разных поставщиков поступают четыре партии различных видов мебели, из которых комплектуются гарнитуры. Вероятности того, что партии товара будут доставлены в срок, равны соответственно 0,9; 0,8; 0,7 и 0,95. Найти вероятность того, что хотя бы одна партия не будет доставлена в срок.

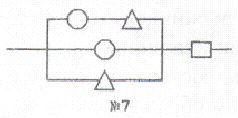
Задача 3198. Вычислить надежность схемы, полагая, что надежность круглых элементов равна 0,9, прямоугольных – 0,8 и треугольных - 0,75.

Задача 3199. Три стрелка стреляют в цель независимо друг от друга. Первый стрелок попадает в цель с вероятностью 0,6, второй – с вероятностью 0,7, а третий – с вероятностью 0,75. Найти вероятность хотя бы одного попадания в цель, если каждый стрелок сделает по одному выстрелу.

Задача 3200. В первом ящике 4 черных и 2 белых шара, во втором 3 черных и 5 белых. Из первого наудачу извлекают один. Из второго два шара. Найдите вероятность того, что шары одного цвета.

Задача 3201. Вероятность того, что в страховую компанию в течение года обратится с иском о возмещении ущерба первый клиент, равна 24/100. Для второго клиента вероятность такого обращения равна 29/100. Для третьего клиента - 19/100. Найти вероятность того, что в течение года в страховую компанию обратится хотя бы один клиент, если обращения клиентов - события независимые.

Задача 3202. Бросаются три игральных кубика. Найти вероятности событий:
А – на всех кубиках в сумме выпало ровно четыре очка;
В – на всех кубиках в сумме выпало не менее четырех очков;
С – на всех кубиках в сумме выпало более четырех очков.

Задача 3203. Разрыв электрической цепи происходит в том случае, когда выходит из строя хотя бы один элемент из трех последовательно соединенных. Определить, что не будет разрыва цепи, если элементы выходят из строя соответственно с вероятностью 0.3; 0.4; 0.6.

Задача 3204. В группе спортсменов два мастера спорта, шесть кандидатов в мастера и восемь перворазрядников. По жребию выбирается четыре спортсмена. Найти вероятность событий:
А – все четыре выбранные спортсмена оказались кандидатами в мастера спорта,
В – среди выбранных спортсменов хотя бы один оказался кандидатом в мастера спорта,
С – среди выбранных спортсменов оказалось два мастера спорта и два кандидата в мастера спорта.

Задача 3205. Брошена монета и игральная кость. Найти вероятность совмещения событий: «появился герб», «появилось 6 очков».

< Предыдущая 1 2 3 4 5 6 ... 47 Следующая > 

* Конечная стоимость зависит от комиссии выбранного вами варианта оплаты и будет указана перед оплатой.