< Предыдущая 1 ... 4 5 6 7 8 ... 47 Следующая > 

События. Теоремы сложения и умножения

Решения задач с 3258 по 3311

Задача 3258. Дано: P(A+B)=0.6, P(AB)=0.3, P(A|B)=0.6. Найти P(A), P(B), P(B|A), выяснить, зависимы ли события A, B.

Задача 3259. Артиллерийское орудие ведет стрельбу по приближающейся цели, располагая тремя снарядами. Вероятность попадания в начале стрельбы 0,4 и увеличивается на 0,1 при каждом следующем выстреле. Какова вероятность двух попаданий при трех выстрелах?

Задача 3260. Экзаменационные билеты (20) содержат по 2 вопроса, которые не повторяются. Студент может ответить только на 30 вопросов. Определить вероятность сдачи экзамена, если для этого нужно ответить на 2 вопроса из одного билета или на 1 вопрос из одного и на дополнительный 2-ой вопрос из другого билета.

Задача 3261. Вероятность поражения цели хотя бы одной пулей при 4 независимых выстрелах равна 0,59. Какова вероятность поражения цели при одном выстреле?

Задача 3262. В урне содержится 7 белых, 5 черных и 8 красных шаров. Шары выбираются наугад, причем белый или черный шар в урну не возвращается, а извлеченный из нее красный шар после проверки его цвета укладывается назад в урну. Найти вероятность того, что среди двух последовательно вынутых шаров будет один черный.

Задача 3263. Во время эстафетных соревнований по биатлону каждому участнику требуется поразить на огневом рубеже 5 мишеней, имея для этого 7 патронов. Вероятность попадания в мишень при выстреле составляет 0,8. Определить вероятность того, что все мишени будут поражены ровно семью патронами.

Задача 3264. В волейбольном матче игра происходит до тех пор, пока одна из команд не выиграет трех партий. Вероятность победы команды А в каждой партии равна 0,4. Определить вероятность того, что команда Б победит со счетом 3:0.

Задача 3265. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое – 0,8, для второго и третьего – 0,9 и 0,8 соответственно. Найти вероятность того, что при аварии сработает только одно устройство.

Задача 3266. Четыре пловца взяли старт на соревнованиях по плаванию. Вероятность уложиться в рекордное время у первого пловца равна 0,95, у второго – 0,92, у третьего – 0,9, у четвертого – 0,88. Найти вероятность того, что:
1) все пловцы станут рекордсменами;
2) только два пловца станут рекордсменами.

Задача 3267. Имеется три ящика, в первом из которых 6 стандартных и 3 бракованных детали, во втором – 5 стандартных и 4 бракованных и в третьем – 7 стандартных и 4 бракованных. Определить вероятность того, что если из каждого ящика выбрать по детали, то среди них будет одна стандартная и две бракованных.

Задача 3268. Для поражения трех целей орудие может произвести не более 8 выстрелов. Вероятность поражения цели при каждом выстреле равна 0,4. Найти вероятность того, что будут израсходованы все снаряды.

Задача 3269. Решить задачу, применяя теоремы сложения и умножения.
Контролер ОТК, проверив качество сшитых 20 пальто, установил, что 16 из них первого сорта, а остальные – второго. Найти вероятность того, что среди взятых наудачу двух пальто из этой партии
А) одно будет второго сорта,
Б) хотя бы одно первого сорта.

Задача 3270. Прибор А дублируется прибором В. При выходе из строя прибора А происходит переключение на прибор В. Вероятность безотказной работы приборов А и В p=0.8, а переключателя - p1=0.9. Найти вероятность безотказной работы системы в целом.

Задача 3271. Вероятность попадания в цель для каждого из трех стрелков соответственно равны: 0,5; 0,7; 0,75. каждый стрелок сделал по выстрелу. Найти вероятность того, что будет ровно два попадания.

Задача 3272. Решить задачу, применяя теоремы сложения и умножения.
По результатам проверки контрольных работ оказалось, что в первой группе получили положительные оценки 20 студентов из 30, а во второй – 15 из 25. Найти вероятность того, что из наудачу выбранных двух работ:
А) только одна имеет положительную оценку,
Б) ни одна не имеет положительную оценку.

Задача 3273. Пусть вероятность попадания в движущуюся цель при одном выстреле постоянна и равна 0,05. Сколько необходимо сделать выстрелов для того, чтобы с вероятностью, не меньшей 0,75, иметь хотя бы одно попадание.

Задача 3274. Для выполнения задания направлены три пары работников. Каждая пара выполняет свою часть заданий, которое будет успешным лишь при выполнении всех частей. В парах работники действуют независимо, и достаточно одному из них выполнить возложенную на каждого из них часть задания. Вероятность выполнения своей части задания каждым работником первой пары равна 0,8, второй – 0,75, третьей – 0,4. Какова вероятность того, что задание в целом будет выполнено.

Задача 3275. Из полного набора костей домино выбирается кость, затем она возвращается обратно и извлекается еще одна кость. Найти вероятность того, что на обеих костях нет цифр 4 и 0.

Задача 3276. Орудие осуществляет стрельбу по цели, для поражения которой необходимо попасть в нее дважды. Вероятность попадания в цель при первом выстреле равна 0,2, в дальнейшем она не меняется при промахах, но после первого попадания вероятность промаха при дальнейших выстрелах уменьшается вдвое. Боекомплект составляет 8 снарядов. Найти вероятность того, что цель будет повреждена, но не поражена.

Задача 3279. Два студента сдают задачку на зачете по математике преподавателю. Вероятность того, что сдаст первый студент равна 0,8, а второй – 0,4. С какой вероятностью они оба сдадут эту задачу? А хотя бы один из них?

Задача 3280. В волейбольном матче игра происходит до тех пор, пока одна из команд не выиграет трех партий. Вероятность победы команды A в каждой партии равна 0,5. Определить вероятность того, что в матче победит команда A.

Задача 3281. Орудие осуществляет стрельбу по цели, для поражения которой необходимо попасть в нее дважды. Вероятность попадания в цель при первом выстреле равна 0,4, а в дальнейшем она не меняется при промахах, но после первого попадания вероятность промаха при дальнейших выстрелах уменьшается вдвое. Определить вероятность того, что за первые три выстрела будет ровно одно попадание.

Задача 3282. В ящике содержится 8 деталей типа А, 4 – типа Б и 6 – типа В. Детали выбираются наугад, причем вытащенная деталь типа А или Б откладывается в сторону, а извлеченная деталь типа В возвращается назад в ящик. Определить вероятность того, что если выбрать две детали, то среди них не будет типа А.

Задача 3283. Вероятность безотказной работы в течение времени T каждого элемента равна p. Элементы работают независимо и включены в цепь по схеме. Найти вероятность, что в течение времени T ток в цепи не прекратится.

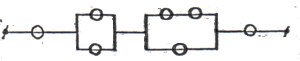
Задача 3284. Три покупателя заходят в магазин, независимо друга делают не более одной покупки. Вероятность покупки каждым покупателем 0.8,0.7,0.6. Найти вероятность того, что после захода этих трех покупателей будет совершена ровно одна покупка.

Задача 3285. Трое охотников увидели утку и одновременно выстрелили. Вероятности попадания для них соответственно равны p1=0.5, p2=0.7, p3=0.4. Какова вероятность, что утка будет
А) убита двумя пулями,
Б) убита.

Задача 3287. В волейбольном матче игра происходит до тех пор, пока одна из команд не выиграет трех партий. Вероятность победы команды A в каждой партии равна 0,8. Определить вероятность того, что в матче победит команда A.

Задача 3288. Орудие осуществляет стрельбу по цели, для поражения которой необходимо попасть в нее дважды. Вероятность попадания в цель при первом выстреле равна 0,4, а в дальнейшем она не меняется при промахах, но после первого попадания вероятность промаха при дальнейших выстрелах уменьшается вдвое. Боекомплект составляет 5 снарядов. Определить вероятность того, что цель будет поражена, если первый выстрел был точным.

Задача 3289. В ящике содержится 3 детали типа А, 7 – типа Б и 6 – типа В. Детали выбираются наугад, причем вытащенная деталь типа А или Б откладывается в сторону, а извлеченная деталь типа В возвращается назад в ящик. Определить вероятность того, что если выбрать две детали, то они будут разных типов.

Задача 3290. Три стрелка стреляют по мишени. Предполагается, что события попадания в мишень для стрелков независимы и вероятности попадания стрелков в мишень равны p1, p2, р3. Какова вероятность того, что:
а) все три выстрела окажутся успешными;
б) хотя бы один из трёх выстрелов окажется успешным;
в) точно один выстрел окажется успешным, два неуспешными?
p1=0.9, p2=0.8, p3=0.7.

Задача 3292. Пусть А, В, С — случайные события. Выяснить смысл равенств: А U В U С = А.

Задача 3293. Почтальон вложил в 2 почтовых ящика по 20 корреспонденций. В первый ящик 17 писем и 3 открытки, во второй 18 писем и 2 открытки. Наугад из двух ящиков выбирают по 1 корреспонденции. Какова вероятность того, что обе вынутые корреспонденции оказались открытками?

Задача 3294. Охотник выстрелил три раза по удаляющейся цели. Вероятность попадания в нее в начале стрельбы равна 0,6, а после каждого выстрела уменьшается на 0,1. Найти вероятность того, что охотник попадает хотя бы один раз.

Задача 3295. Какова вероятность того, что при одиннадцати бросаниях монеты герб выпадет по крайней мере девять раз подряд?

Задача 3296. Два баскетболиста последовательно кидают мяч в корзину. Вероятность того, что при этом будет ровно одно попадание равна 0,55. Найти вероятность попадания в кольцо вторым баскетболистом, если известно, что первый промахивается с вероятностью 0,3.

Задача 3297. Каждый прибор проходит два испытания. Вероятность выхода из строя прибора при первом испытании равна p1, при втором - p2. Испытано n приборов. Найти вероятность, что из строя вышло не более одного прибора.

Задача 3298. Завод в среднем даёт 27% продукции высшего сорта к 70% первого сорта. Найти вероятность того, что наугад взятое изделие будет или высшего, или первого сорта.

Задача 3299. Статистика, собранная среди студентов одного из вузов, обнаружила следующие факты: 60% всех студентов занимаются спортом, 40% участвуют в научной работе на кафедрах и 20% занимаются спортом и участвуют в научной работе на кафедрах. Корреспондент местной газеты подошел к наудачу выбранному студенту. Найти вероятность следующих событий:
A = {студент занимается по крайней мере одним из указанных видов деятельности},
B = {студент занимается одним только спортом},
C = {студент занимается только одним видом деятельности}.

Задача 3300. Три стрелка стреляют в одну мишень; вероятность попадания с одного выстрела равна: 0,8 – у 1 стрелка, 0,6 - у 2-го, 0,5 – у 3-го. Найти вероятность появления в мишени не менее одной пробоины в результате одновременного выстрела всех трех стрелков.

Задача 3301. В сосуде 11 шаров, из которых 4 цветных и 7 белых. Найти вероятность двукратного извлечения из сосуда белого шара:
А) если вынутый шар возвращается обратно в сосуд и
Б) если вынутый шар в сосуд не возвращается.

Задача 3302. Решить задачу, используя теоремы сложения и умножения. Студент будет отчислен, если он трижды не сдаст экзамен. Какова вероятность не быть отчисленным у студента, который может сдать экзамен с вероятностью 0,6?

Задача 3303. Больному рекомендованы два препарата, которые дают нежелательнй эффект в 2% и 4% случаях соответственно. Найти вероятность, что при приеме этих лекарств (обоих вместе), одно из лекарств дало нежелательный эффект.

Задача 3304. Вероятность успешно выполнить упражнение для каждого из двух спортсменов равна 0,6. Спортсмены выполняют упражнение по очереди, делая по две попытки. Выполнивший первым упражнение успешно получает приз. Найти вероятность того, что приз будет вручен.

Задача 3305. В первой лотерее из 34 билетов 20 выигрышных, во второй – из 25 билетов 15 выигрышных. Наугад выбирают по одному билету из каждой лотереи. Какова вероятность того, что хотя бы один билет будет выигрышным?

Задача 3306. Из цифр 1, 2, 3, 4, 5, 6, 7 выбирают два и составляют двузначное число. Событие А — обе цифры четные, В — обе нечетные. Найти вероятность событий:

Задача 3307. Вероятность поражения цели первым стрелком при одном выстреле равна 0,8, а вторым — 0,6. Найти вероятность того, что цель будет поражена только одним стрелком.

Задача 3308. На аукцион выставлены акции трёх компаний. Вероятность того, что будет продан пакет акций первой компании 0,7, для второй 0,9, для третьей 0,8. Найти вероятность того, что в результате торгов будут проданы пакеты акций m компаний, где m≤1.

Задача 3309. По танкам ведут огонь 2 гранатометчика. Вероятность попадания первого равна 0,9, второго - 0,6. Производится по одному выстрелу из каждого гранатомета. Определить вероятность того, что будет два промаха.

Задача 3310. Принимая вероятность рождения однополых близнецов вдвое большей, чем разнополых, вероятности рождения близнецов разного пола в любой последовательности одинаковыми, а вероятность рождения в двойне первым мальчика равной 0,51, определить вероятность рождения второго мальчика, если первым родился мальчик.

Задача 3311. Радист трижды вызывает корреспондента. Вероятность того, что корреспондент примет первый вызов, равна 0,2, второй – 0,3 и третий – 0,4. По условиям приема события, состоящие в том, что i-й по счету вызов (i = 1, 2, 3) услышан, независимы. Найти вероятность того, что корреспондент вообще услышит радиста.

< Предыдущая 1 ... 4 5 6 7 8 ... 47 Следующая > 

* Конечная стоимость зависит от комиссии выбранного вами варианта оплаты и будет указана перед оплатой.