< Предыдущая 1 ... 5 6 7 8 9 ... 47 Следующая > 

События. Теоремы сложения и умножения

Решения задач с 3312 по 3361

Задача 3312. Стрелок А попадает в мишень с вероятностью 0,4, стрелок В – с вероятностью 0,3. У каждого из них по два патрона. Стреляют по очереди по одному выстрелу. Первым – стрелок В. Выигрывает тот, кто первый попадёт в мишень.
а) Какова вероятность того, что выиграет стрелок А?
б) Какова вероятность того, что выиграет стрелок В?

Задача 3313. При включении зажигания двигатель начинает работать с вероятностью 0,6. Найти вероятность того, что:
А) двигатель начинает работать при третьем включении зажигания;
Б) для запуска двигателя придется включить зажигание не более трех раз.

Задача 3314. Вероятность своевременного выполнения студентом контрольной работы по каждой из трех дисциплин равна соответственно 0,6, 0,5 и 0,8. Найти вероятность своевременного выполнения контрольной работы студентом:
А) по двум дисциплинам;
Б) хотя бы по двум дисциплинам.

Задача 3315. Три стрелка стреляют по мишени. Вероятности попадания в мишень для них соответственно равны 0,7; 0,5; 0,8. Какова вероятность, что в мишень:
а) попадут два стрелка;
б) мишень будет поражена?

Задача 3316. В волейбольном матче игра происходит до тех пор, пока одна из команд не выиграет трех партий. Вероятность победы команды А в каждой партии равна 0.8. Определить вероятность того, что команда Б победит со счетом 3:0.

Задача 3317. Вероятность того, что футбольная команда выиграет в 1/8 финала - 0.9, в 1/4 финала - как 0,6, и в 1/2 финала - как 0,5. Какова вероятность того, что команда будет играть в финале? Какова вероятность того, что команде не удастся выйти в финал?

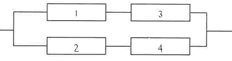
Задача 3318. Найти вероятность отказа цепи, если вероятности отказа элементов соответственно равны q1=0.01, q2=0.02, q3=0.01, q4=0.01.

Задача 3319. Брошены две игральные кости. Предполагается, что все комбинации выпавших очков равновероятны. Найти условную вероятность того, что выпали две пятерки, если известно, что сумма выпавших очков делится на пять.

Задача 3320. Дано: два одинаковых ящика. В первом ящике три белых шарика и два красных, во втором пять красных и два белых. С какой вероятностью:
1) Вынимая из каждого ящика по одному шарику мы вынем шары одного цвета
2) Вынимая из каждого ящика по два шарика мы вынем шары одного цвета.

Задача 3321. При включении зажигания двигатель начинает работать с вероятностью р. Найти вероятность того, что двигатель заведется при втором включении стартера.

Задача 3322. При включении стартера двигатель начинает работать с вероятностью p. Найти вероятность того, что для включения двигателя потребуется не более 2-х попыток.

Задача 3323. В коробке 20 синих и 20 красных шаров. Вынуты 4 шара. Найти вероятность того, что синих оказалось больше.

Задача 3324. Найти вероятность отказа цепи, если вероятности отказа элементов соответственно равны q1=0.02, q2=0.03, q3=0.02, q4=0.03.

Задача 3325. На школьном участке посадили три плодовых дерева: яблоню, грушу и сливу. Вероятность того, что приживется яблоня, равна 0,8, груша – 0,9, слива – 0,7. Найти вероятность того, что
А) приживутся два дерева;
Б) приживется хотя бы одно дерево.

Задача 3326. На первой полке стоят 30 книг по математике, из них 10 учебников, на второй полке 20 книг, по физике из них 5 учебников, с обеих полок наугад берут по 1 книге.
Чему равна вероятность того, что обе книги будут учебником?

Задача 3327. Технический контроль проверяет четыре изделия. Пусть Ai, i=1,2,3,4 - события, означающие наличие дефекта в i-м изделии. Записать событие: с дефектами оказались не более двух изделий.

Задача 3328. В волейбольном матче игра происходит до тех пор, пока одна из команд не выиграет трех партий. Вероятность победы команды А в каждой партии равна 0,7. Определить вероятность того, что команда А победит со счетом 3:1.

Задача 3329. В двух урнах находятся шары, отличающиеся только цветом, причем в первой урне 5 белых шаров, 11 черных и 8 красных, а во второй соответственно 10, 8 и 6. Из обеих урн наудачу извлекается по одному шару. Какова вероятность того, что оба шара одного цвета?

Задача 3330. Имеется три ящика, в первом из которых 6 стандартных и 4 бракованных детали, во втором – 5 стандартных и 7 бракованных, а в третьем – 8 стандартных и 8 бракованных. Определить вероятность того, что если из каждого ящика выбрать по детали, то все они будут стандартными.

Задача 3331. В театральной кассе к некоторому моменту времени остались: 1 билет в театр эстрады, 2 билета в драматический театр и 3 билета в театр комедии. Каждый очередной покупатель приобретает лишь один билет в любой из возможных театров. Два человека из очереди последовательно приобрели билеты.
Найти вероятность того, что: куплены билеты в один какой-нибудь театр.

Задача 3332. В магазине 20 цветных и 30 ч/б телевизоров. Дополнительной регулировки требуют 2 цветных и 6 ч/б телевизора. Наугад взяли по одному телевизору из каждой группы. Найти вероятность того, что регулировки требуют: а) только ч/б телевизор, б) оба телевизора.

Задача 3333. Только 1 из 5 ключей подходит к данной двери. Найти вероятность того, что для открывания двери придется опробовать ровно 4 ключа.

Задача 3334. Вероятность того, что студент сдаст первый экзамен, равна 0,9, второй — 0,9, третий — 0,8. Найти вероятность того, что студент сдаст: а) только 2-й экзамен, б) только один экзамен, в) три экзамена, г) по крайней мере, два экзамена, д) хотя бы один экзамен.

Задача 3335. Причиной отказа электрической схемы в целом могут быть либо выход из строя одного элемента К1, либо выход из строя двух элементов К2 и К3. Элементы могут выходить из строя независимо с вероятностями, равными соответственно 0,1, 0,2, 0,3. Какова вероятность отказа электрической схемы в целом?

Задача 3336. Производительности трёх станков, обрабатывающих одинаковые детали, относятся как 1:3:6. Из нерассортированной партии обработанных деталей взяты наудачу две. Какова вероятность того, что:
а) одна из деталей обработана на 3-м станке,
б) обе обработаны на одном станке?

Задача 3337. Экзаменационный билет состоит из 10 вопросов — по 2 вопроса из 20 по каждой из пяти тем, представленных в билете. По каждой теме студент знает половину всех вопросов. Какова вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на один вопрос по каждой из пяти тем в билете?

Задача 3338. При любой попытке запуска двигатель автомобиля начинает работать с вероятностью 0,6. Найти вероятность того, что
а) двигатель запустится с третьей попытки,
б) трёх попыток будет достаточно,
в) двух попыток будет недостаточно.

Задача 3339. Брошены две игральные кости. Событие А = {выпадение шестёрки на первой кости}. Событие В = {сумма выпавших очков равна 7}. Являются ли события А, В независимыми?

Задача 3340. Три стрелка стреляют по цели. Вероятность попадания в цель для первого стрелка – 0,75, для второго – 0,8, для третьего – 0,9. Какова вероятность того, что хотя бы один стрелок попадет в цель?

Задача 3341. Из шести карточек с буквами Л, И, Т, Е, Р, А выбирают наугад в определенном порядке четыре. Найдите вероятность того, что при этом получится слово «ТИРЕ».

Задача 3342. Игральная кость подбрасывается дважды. Найдите вероятность того, что хотя бы раз выпадет больше четырех.

Задача 3343. вероятностное пространство, . Запишите событие: произошло только событие А.

Задача 3344. Электрическая цепь составлена по схеме, приведенной на рисунке. Событие A_k элемент с номером k вышел из строя. Событие А – разрыв цепи. Вероятность отказа k-го элемента равна p_k. Найдите .

Задача 3345. Даны три события: A - студент учится на первом курсе; B - студент живет в общежитии; С – студент вовремя сдал сессию. Что означает событие: ? Изобразите это событие с помощью диаграммы Венна.

Задача 3346. Рабочий обслуживает 3 станка. Вероятность того, что в течение смены его внимания потребует первый станок, равна 0,7; второй - 0,75 и третий - 0,8. Найти вероятность того, что в течение смены его внимания потребуют какие-либо два станка.

Задача 3347. На станцию прибыло пять тракторов Челябинского и четыре трактора Павлодарского тракторных заводов. Представитель УМС последовательно забирает два трактора. Найти вероятность того, что первый трактор Челябинского завода, а второй – Павлодарского.

Задача 3348. Производятся испытания грузового автомобиля с увеличением веса груза. Вероятность того, что автомобиль выдержит установленные нормы при первом испытании, равна 0,9, при втором – 0,6, при третьем – 0,3. Найти вероятность того, что
А) грузовик выдержит все испытания,
Б) грузовик выдержит два испытания,
В) не выдержит ни одного испытания.

Задача 3349. Вероятность, что в течение одной смены возникает неполадка станка, равна 0.05. Какова вероятность того, что за три смены не произойдет ни одной неполадки.

Задача 3350. Партия из ста деталей подвергается выборочному контролю. Условием непригодности всей партии является наличие хотя бы одной дефектной детали среди четырех проверяемых. Какова вероятность того, что данная партия не будет принята, если она содержит 3% дефектных деталей?
Теоремы сложения и умножения вероятностей.

Задача 3351. Устройство состоит из трех элементов, работающих независимо. Вероятность безотказной работы (за время t) первого, второго и третьего элементов соответственного равны 0,6, 0,7 и 0,8. Найти вероятность того, что за время безотказно будут работать:
а) только один элемент;
б) только два элемента;
в) все три элемента.

Задача 3352. Завод изготавливает 95% стандартных изделий, причем из них 86% первого сорта. Найти вероятность того, что изделие, изготовленное на этом заводе, окажется первого сорта.

Задача 3353. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.

Задача 3354. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное.

Задача 3355. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность.

Задача 3356. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех проверенных изделий только два изделия высшего сорта.

Задача 3357. Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы (за время t) первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что за время t безотказно будут работать: а) только один элемент; б) только два элемента; в) все три элемента.

Задача 3358. Вероятности того, что нужная сборщику деталь находится в первом, втором, третьем, четвертом ящике, соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероятности того, что деталь содержится: а) не более чем в трех ящиках; б) не менее чем в двух ящиках.

Задача 3359. Брошены три игральные кости. Найти вероятности следующих событий:
а) на каждой из выпавших граней появится пять очков;
б) на всех выпавших гранях появится одинаковое число очков.

Задача 3360. Брошены три игральные кости. Найти вероятности следующих событий:
а) на двух выпавших гранях появится одно очко, а на третьей грани – другое число очков;
б) на двух выпавших гранях появится одинаковое число очков, а на третьей грани – другое число очков;
в) на всех выпавших гранях появится разное число очков.

Задача 3361. В круг радиуса R вписан правильный треугольник. Внутрь круга наудачу брошены четыре точки. Найти вероятности следующих событий: а) все четыре точки попадут внутрь треугольника; б) одна точка попадет внутрь треугольника и по одной точке попадет на каждый «малый» сегмент. Предполагается, что вероятность попадания точки в фигуру пропорциональна площади фигуры и не зависит от ее расположения.

< Предыдущая 1 ... 5 6 7 8 9 ... 47 Следующая > 

* Конечная стоимость зависит от комиссии выбранного вами варианта оплаты и будет указана перед оплатой.