< Предыдущая 1 ... 7 8 9 10 11 ... 47 Следующая > 

События. Теоремы сложения и умножения

Решения задач с 3415 по 3471

Задача 3415. В двух урнах находятся шары. В первой урне: 5 белых, 4 черных, 8 красных шаров. Во второй урне 10 белых, 8 черных и 6 красных шаров. Из каждой урны взяли по одному шару. Определить вероятность того что шары будут одинакового цвета.

Задача 3416. Дано устройство, состоящее из нескольких элементов. Схема устройства приведена на рисунке, вероятность отказа каждого элемента известна. Устройство работает, если существует хотя бы одна цепочка из исправных элементов, соединяющая точки и . Найти вероятность отказа устройства.

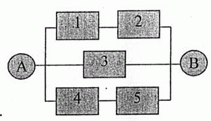
Задача 3418. Для получения кредита предприятие обратилось к трем банкам. Статистические исследования показали, что вероятности выделения кредита этими банками оценивается следующим образом: для первого банка p1=1/6, для второго банка p2=1/8 и для третьего банка p3=1/10. Банки выделяют кредит независимо друг от друга и, если примут решение о его выделении, в размере: первый банк - 20 млн. руб., второй - 10 млн. руб., третий - 30 млн. руб. Рассмотрим следующие события: А - первый банк выделил кредит; В - второй банк выделил кредит; С - третий банк выделил кредит. Интересы предприятия, обратившегося за кредитом, описываются событиями D – получен кредит 30 млн. руб. и Е – получен кредит не менее 50 млн. руб. Выразить эти события через события А, В, С и найти их вероятности.

Задача 3419. Сколько раз нужно бросить две игральные кости, чтобы с вероятностью не меньше 0,5, хотя бы один раз на двух костях появилась сумма очков, равная 12?

Задача 3420. Установить, являются ли случайные события независимыми, используя понятие условной вероятности. Игральная кость бросается два раза. X1 и X2 – числа выпавших очков. Рассматриваются события
A1 : X1 делится на 2; X2 делится на 3;
A2 : X1 делится на X2.
Являются ли эти события зависимыми?

Задача 3422. Два бомбардировщика преодолевают зону ПВО. Вероятность того, что будет сбит первый, равна 0.7; что сбит второй, равна 0.8. Найти вероятность:
а) уничтожения одного бомбардировщика;
б) поражения двух бомбардировщиков;
в) промахов.

Задача 3423. Вычислить надежность схемы, полагая, что надежность круглых элементов равна 0,9, прямоугольных – 0,8 и треугольных – 0,75.

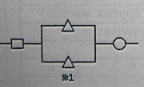
Задача 3424. В ящике смешаны нити трех цветов: белых – 50%, красных – 30%, черных – 20%. Определить вероятность того, что при последовательном вытягивании наугад трех нитей окажется:
А) все нити одного цвета;
Б) все нити разных цветов;
В) две нити одного цвета.

Задача 3425. Два охотника одновременно увидели лису и одновременно выстрелили в нее. Каждый из этих охотников на таком расстоянии обычно в одном случае из трех попадает в лису и убивает ее. Какова вероятность того, что лиса будет убита?

Задача 3426. Производится испытание трех электрических чайников, работающих независимо друг от друга. Длительности времени безотказной работы чайников (плотность распределения) распределены по показательному закону: для первого чайника f1(t)=0.02*exp(-0.02t), для второго f2(t)=0.05*exp(-0.05t), для третьего f3(t)=0.06*exp(-0.06t). Найти вероятность, что в интервале времени (0; 13) откажут:
1) все три чайника;
2) хотя бы один чайник;
3) ровно два чайника.

Задача 3428. Вероятность получить достаточного дохода по итогам года для каждого из фермеров равно 0,8. Найти вероятность того, что из выбранных наудачу двух фермеров:
а) один получит достаточный доход;
б) по крайней мере один получит достаточный доход.

Задача 3429. Охотник выстрелил три раза по удаляющейся цели. Вероятность попадания в нее в начале стрельбы равна 0,8, а после каждого выстрела уменьшается на 0,1. Найти вероятность того, что он промахнется все три раза.

Задача 3430. Вероятность выхода из строя электрического прибора равна 0,6. Для повышения надежности работы в прибор наставлено 5 дублирующих цепей. Определить, во сколько раз при этом увеличится надежность работы прибора.

Задача 3431. В урне 2 белых и 3 черных шара. Два игрока поочередно вынимают из урны по шару, не вкладывая их обратно. Выигрывает тот, кто раньше получит белый шар. Найти вероятность того, что выигрывает первый игрок.

Задача 3433. Два стрелка сделали по одному выстрелу по мишени. Вероятность попадания для первого стрелка – 0,7, для второго – 0,6. Какова вероятность, что:
А) оба промахнутся;
Б) оба попадут;
В) хотя бы один попадет;
Г) хотя бы один промахнется.

Задача 3434. Какое минимальное количество монет надо взять, чтобы вероятность получения хотя бы одного «орла» при их подбрасывании была больше 0,99?

Задача 3435. В течение определенного периода две фирмы, работающих на рынке имеют возможность, независимо друг от друга, обанкротиться с вероятностями 0,38 и 0,28. Найдите вероятность того, что:
а) обе фирмы будут работать успешно;
б) обанкротится только одна фирма;
в) хотя бы одна фирма будет успешно функционировать.

Задача 3436. Известны вероятности независимых событий: P(A)=0.7, P(B)=0.4, P(C)=0.5. Определить вероятность того, что:
А) произойдет одно и только одно из этих событий,
Б) произойдет не более двух событий.

Задача 3437. Три стрелка выстрелили по мишени по одному разу. Вероятность попадания для них 0,9; 0,8 и 0,7 соответственно. Найти вероятность, что мишень поражена не более одного раза.

Задача 3438. Обследовано 200 пар отцов с сыновьями с целью проверки, имеется ли зависимость между их профессиями. Среди них оказалось: 40 отцов и 50 сыновей, имеющих некоторую профессию М, 25 сыновей, профессия которых совпадает с профессией отца (относительно профессии М). Найти вероятность того, что:
а) у отца, занимающегося профессией М, сын занимается той же профессией;
б) у отца, не занимающегося профессией М, сын занимается профессией М.

Задача 3439. Вероятность получения билета, у которого равны суммы трёх первых и трёх последних цифр шестизначного номера, равна 0.05525. Какова вероятность иметь такой билет среди двух взятых наудачу, если оба билета: имеют последовательные номера; получены независимо один от другого?

Задача 3440. Три стрелка делают по одному выстрелу в мишень с дальнего расстояния. Вероятность попадания для первого стрелка 0.2, для второго - 0.3, для третьего - 0.4. Найти вероятность того, что по мишени будет хотя бы одно попадание.

Задача 3441. Студент озабочен предстоящими экзаменами по физике, математике и сопротивлению материалов. По его мнению, вероятность того, что он сдаст математику, равна 0,8, а сопротивление материалов - 0,5. Вероятность того, что он сдаст хотя бы один предмет, равна 0,95. Считая сдачу экзаменов независимыми событиями, найти вероятность того, что студент сдаст экзамен по физике. (теорема сложения и умножения)

Задача 3442. Три туриста посетили зал боулинга. Вероятность того, что первый турист собьет все кегли, равна 0,9, второй турист – 0,8, третий – 0,7. Определить вероятность того, что все трое туристов собьют все кегли.

Задача 3444. Фирма по производству претендует на три заказа от трех крупных магазинов (названия). Эксперты фирмы считают, что вероятность получения заказа от магазина № 1 равна 0,78, от магазина №2 - 0,68, от магазина №3 - 0,89. Какова вероятность, что фирма получит заказ.

Задача 3445. Две экономические операции, проводимые предпринимателем одновременно для одной общей цели, имеют вероятности успеха, соответственно равные 0,1 и 0,6. Предприниматель достиг цели. Какова вероятность того, что успех получен в результате: а) первой операции; б) второй операции?

Задача 3446. Электрическая схема состоит из пяти последовательно соединённых блоков. Вероятность безотказной работы каждого блока составляет 0.3, 0.5, 0.8, 0.1, 0.2. Считая выходы из строя различных блоков независимыми событиями, найти надёжность всей схемы в целом.

Задача 3447. Два стрелка производят по одному выстрелу в одну и ту же мишень. Вероятность попадания 1-м стрелком равна 3/15, 2-м - 11/17. Найти вероятность того, что мишень будет поражена.

Задача 3448. Два стрелка стреляют по мишени, вероятности попаданий 0.9 и 0.8. Найти вероятности следующих событий:
1. Оба попадут;
2. Оба промахнутся;
3. Один попадет;
4. Хотя бы один попадет.

Задача 3449. Стрелок стреляет по движущейся мишени до первого попадания, но успевает сделать не более пяти выстрелов. Вероятность попадания в цель при одном выстреле 0,7. Найти вероятность того, что он стрелял
А) один раз;
Б) два раза;
В) пять раз.

Задача 3450. Для производственной практики на 30 студентов предоставлено 15 мест в Сочи, 8 в Туапсе и 7 – в Адлере. Какова вероятность того, что 2 определенных студента попадут на практику в один город?

Задача 3452. Два судьи, выслушав все доводы по рассматриваемому вопросу, независимо друг от друга принимают решения. Анализ 600 ранее рассмотренных аналогичных дел каждым из этих судей, показал, что первый судья вынес ложное решение в 124 раз случаях, а второй судья – в 77 раз случаях. Пусть событие Аi (i=1,2) заключается в том, что i - судья вынесет истинное решение. С помощью операций действий с событиями записать следующие события и найти их вероятности
1) Оба судьи вынесут ложное решение;
2) Первый судья вынесет истинное решение, а второй судья - ложное;
3) Второй судья вынесет истинное решение, а первый судья - ложное;
4) Оба судьи вынесут истинное решение;
5) Оба судьи вынесут одинаковое решения;
6) Судьи вынесут разные решения.

Задача 3453. Рабочий обслуживает три станка. Вероятность выхода из строя за смену для них, соответственно, равна 0,75; 0,8 и 0,7. Найти вероятность того, что за смену выйдут из строя точно два станка.

Задача 3454. Схема содержит три блока типа A, два блока типа B и пять блоков типа C. Схема выходит из строя при порче любого блока. Блоки типа A выходят из строя с вероятностью 0.2, блоки типа B – с вероятностью 0.3, блоки типа C – с вероятностью 0.5. Найти вероятность выхода схемы из строя.

Задача 3455. Среди десяти документов три оформлены не по стандарту. Документы проверяют один за другим до выявления всех нестандартных. Какова вероятность того, что проверка закончится на 5 документах?

Задача 3456. Три орудия ведут огонь по цели. Вероятность попадания в цель из первого орудия – 0,5, из второго – 0,6, из третьего – 0,7. Зная, что каждое орудие стреляет один раз, найти:
А) вероятность поражения цели, если для этого достаточно двух попаданий,
Б) вероятность хотя бы одного попадания.

Задача 3457. Происходит воздушный бой между двумя самолетами: истребителем и бомбардировщиком. Стрельбу начинает истребитель: он делает по бомбардировщику один выстрел и сбивает его с вероятностью 0,2. Если бомбардировщик не сбит, то он стреляет по истребителю и сбивает его с вероятностью 0,25. Если истребитель этим выстрелом не сбит, то он еще раз стреляет по бомбардировщику и сбивает его с вероятностью 0,3. Найти вероятности следующих исходов боя:
А) сбит бомбардировщик,
Б) сбит истребитель,
В) сбит хотя бы один из самолетов.

Задача 3459. Имеются четыре события A1, A2, A3, A4. Выразить в алгебре событий следующее событие: произошло A1 и не более одного из остальных.

Задача 3460. Для поражения цели достаточно двух попаданий. Произведено два залпа из двух орудий, с вероятностями поражения цели 0,45 и 0,6 при одном выстреле. Найти вероятность того, что цель будет поражена.

Задача 3461. В первом ящике 2 белых и 7 черных шаров, во втором ящике 6 белых и 3 черных шара. Из каждого ящика вынули по шару.
а) Какова вероятность того, что оба шара белые?;
б) какова вероятность того, что один из вынутых шаров белый, а другой черный?;
в) какова вероятность того, что шар, вынутый из первого ящика черный, а из второго ящика белый?;
г) какова вероятность того, что шар, вынутый из одного ящика (первого или второго) окажется белым, а шар, вынутый из другого ящика черным?;
д) какова вероятность того, что один из вынутых шаров - синий?

Задача 3462. Вероятность того, что лампа №1 проработает безотказно 100 часов, равна 0,95. Для ламп №2 и №3 эта вероятность соответственно равна 0,85 и 0,75. Для безотказной работы изделия допустим отказ одной лампы. Найти вероятность безотказной работы изделия.

Задача 3463. Пусть A,B,C – три произвольных события. Найти выражения для событий состоящих в том, что из A,B,C
a. произошло только A и В; b. произошло или событие А или событие В, но С не произошло и события А и В не произошли одновременно.

Задача 3464. Может ли симметрическая разность двух событий A и B являться пустым множеством? Ответ обосновать.

Задача 3465. Монета бросается до тех пор, пока два раза подряд она не выпадет одной и той же стороной. Найти вероятность того, что опыт кончится до шестого бросания.

Задача 3466. Рабочий обслуживает 3 станка, работающих независимо друг от друга. Вероятность того, что в течение часа первый станок потребует внимания рабочего, равна 0,02, для второго станка такая вероятность равна 0,1, а для третьего – 0,15. Какова вероятность того, что в течение часа
а) ни один из станков не потребует внимания рабочего;
б) какой-то один потребует внимания.

Задача 3467. У игрока 3 монеты. За 1 ход игрок либо выигрывает, либо проигрывает 1 монету с вероятностью 50%. Найти вероятность победы, если для этого ему нужно выиграть 8 монет.

Задача 3468. Три станка работают независимо. Вероятности того, что в течение смены 1, 2 и 3-й станки выйдут из строя, равны соответственно 0,05; 0,1 и 0,15. Найти вероятность того, что за смену выйдет из строя только один станок.

Задача 3469. Сброшены три бомбы. Мост разрушается при попадании хотя бы одной из них. Вероятности попадания бомб равны 0,3, 0,6 и 0,8. Какова вероятность того, что мост разрушен?

Задача 3470. Два стрелка стреляют по мишени. Первый из них дает промах в 40 выстрелах из 100, второй – в 20. Какова вероятность того, что при однократном залпе попадет хотя бы один стрелок?

Задача 3471. Сколько раз нужно бросить монету, чтобы вероятность хотя бы однократного появления герба была больше 15/16?

< Предыдущая 1 ... 7 8 9 10 11 ... 47 Следующая > 

* Конечная стоимость зависит от комиссии выбранного вами варианта оплаты и будет указана перед оплатой.